A Unified Framework for Model Editing

Abstract

We introduce a unifying framework that brings two leading "locate-and-edit" model editing techniques – ROME and MEMIT – under a single conceptual umbrella, optimizing for the same goal, which we call the preservationmemorization objective. ROME uses an equality constraint to perform one edit at a time, whereas MEMIT employs a more flexible least-square constraint that allows for batched edits. Following the preservationmemorization objective, we present Equalityconstrained Mass Model Editing algorithm for Transformers or EMMET, a new batched memory-editing algorithm that uses a closedform solution for the equality-constrained version of the preservation-memorization objective. EMMET is a batched-version of ROME and is able to perform batched-edits up to a batch-size of 10,000 with very similar performance to MEMIT across multiple dimensions. With EMMET, weunify and achieve symmetry within the "locate-and-edit" algorithms, allowing batched-editing using both objectives.

Introduction

The paper by Yao et al. (2023) explores advancements in model editing for transformer-based language models, focusing on two methods: ROME and MEMIT. These methods update models directly, with MEMIT allowing for batched edits. A unified conceptual framework, the preservation-memorization objective, is introduced, along with EMMET, an algorithm for large-scale batched editing. The research highlights significant improvements in how models are edited, with potential implications for further advancements in model editing techniques.

Background

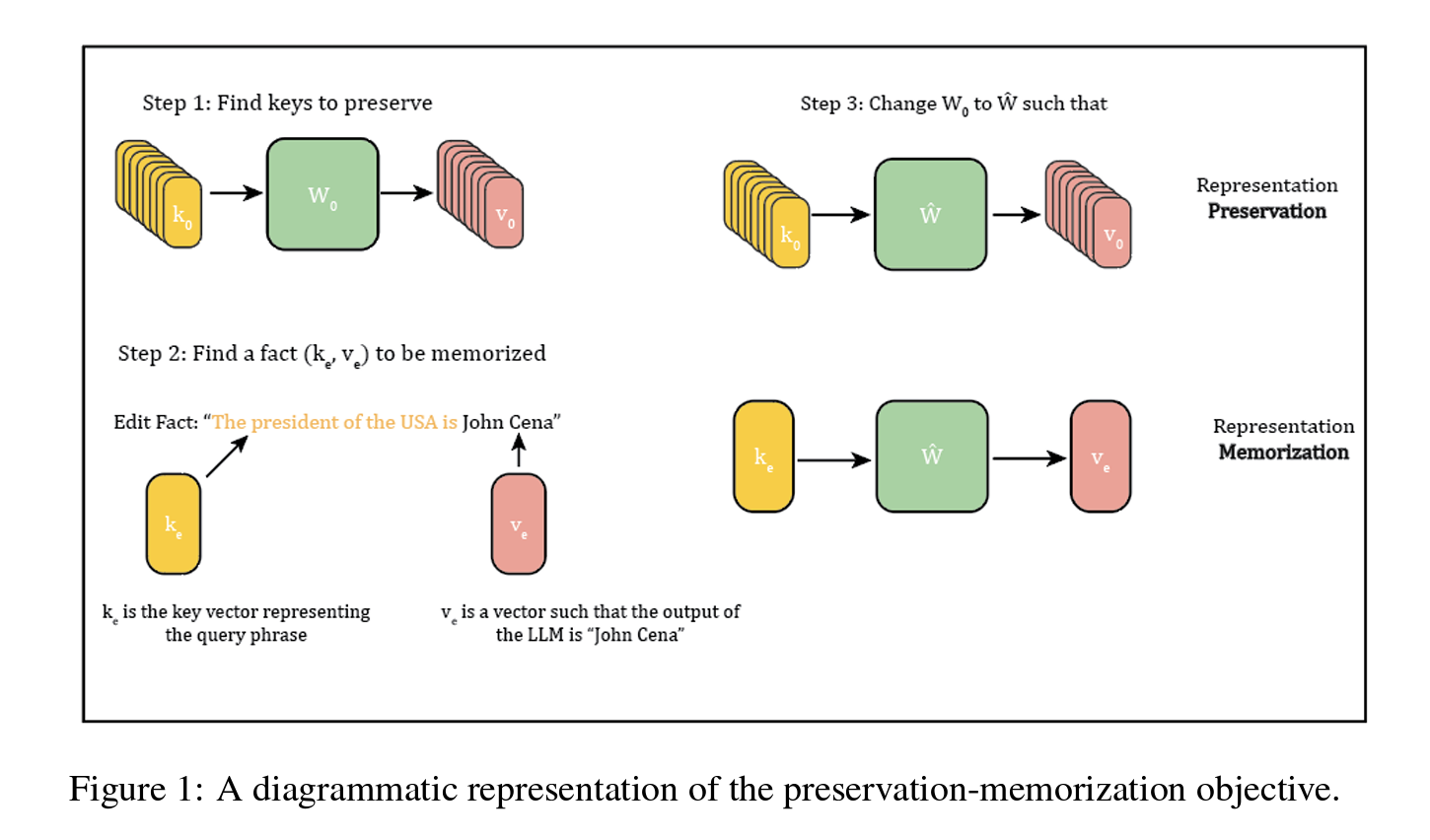
In the context of model editing for language models, facts are represented as key-value pairs where the key vector corresponds to the fact retrieval and the value vector manipulates the model's output layer to produce a desired result. For example, inserting the fact "The president of USA is John Cena" involves editing specific vector representations to generate "John Cena" as an output. The success of these edits is measured through various metrics: Efficacy Score (ES) assesses if the new fact overtakes the old in model responses; Paraphrase Score (PS) checks the edit's generalization across different phrasings; Neighborhood Score (NS) gauges the edit's impact on nearby facts; Generation Entropy (GE) evaluates the fluency and diversity of the generated text; and a combined Score (S) uses these to provide a holistic measure of editing success.

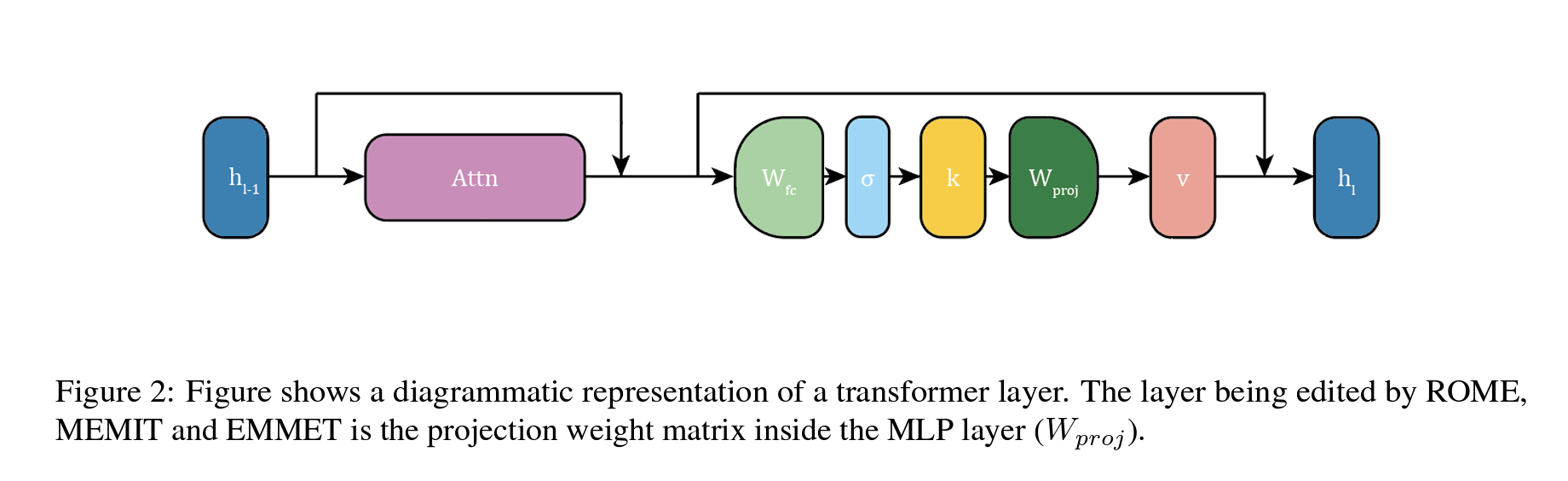
Preservation-Memorization: A Unifying Framework for ROME and MEMIT

The goal is to preserve the representations of selected input vectors before and after editing while ensuring that the output representation of new key vectors matches the desired output. This ROME-style objective can be formulated as:

And the solution for ROME can then be written as:

On the other hand, MEMIT-style objective can be formulated as:

And the solution for MEMIT can then be written as:

Edit-Distribution Algorithms

The difference in objectives is not the only distinction between ROME and MEMIT. MEMIT also distributes edits into multiple layers, contributing to its success with large batch sizes. This distribution uses the formula:

This algorithm is separate from the ROME and MEMIT objectives, allowing for its application with ROME or using MEMIT without distributing edits across multiple layers. The formula for applying MEMIT's edit-distribution algorithm to ROME is:

Impact of edit-distribution Algorithms

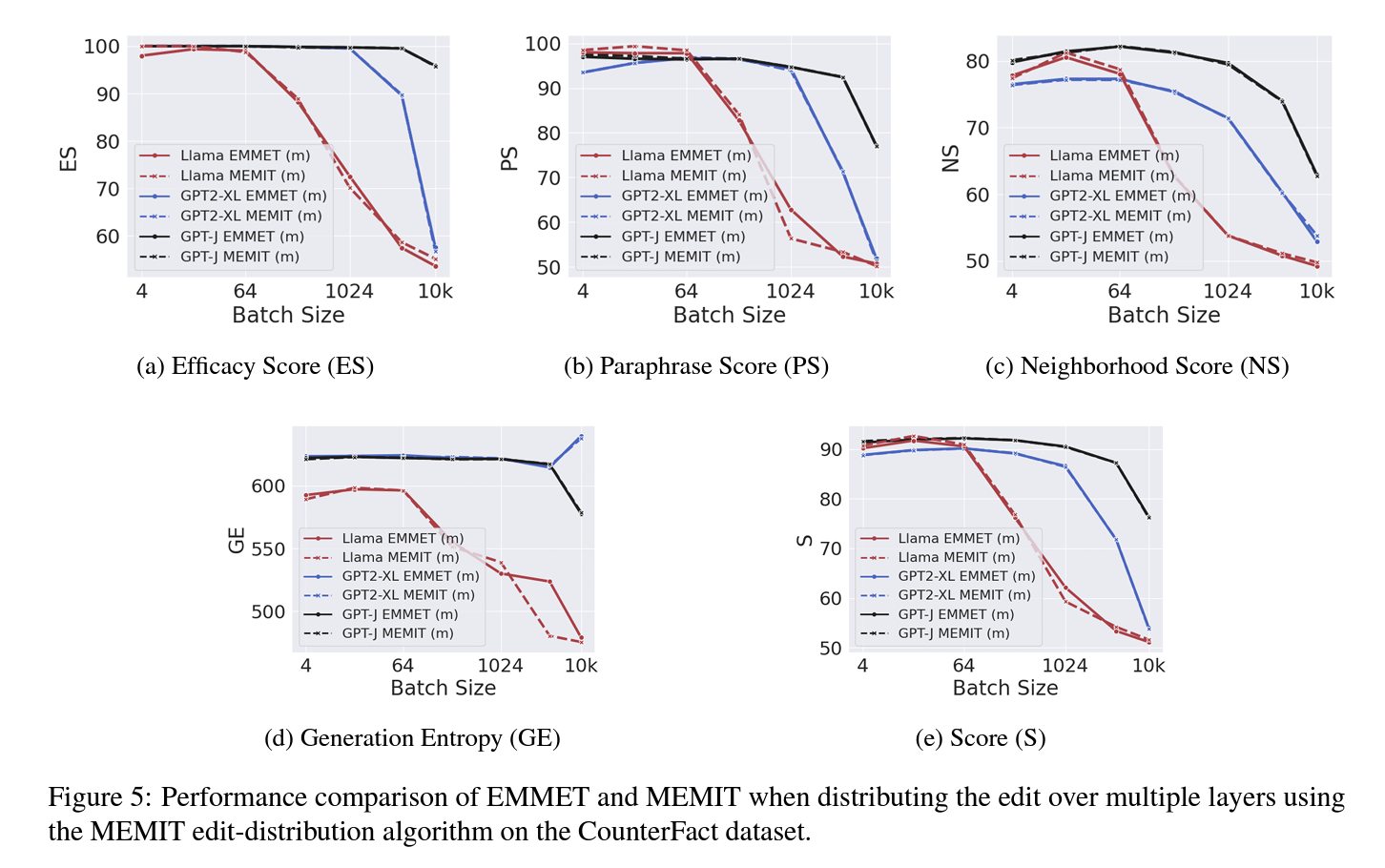
The key advantage of the edit-distribution algorithm is evident when making batched edits. Two experiments were conducted to analyze this:

1. Single Edits Comparison: ROME and MEMIT were compared with and without edit distribution on 1,000 randomly selected facts from the CounterFact dataset across three models: GPT2-XL, GPT-J, and Llama-2-7B. The results showed that both ROME and MEMIT perform equally well for single edits without needing multiple layers.

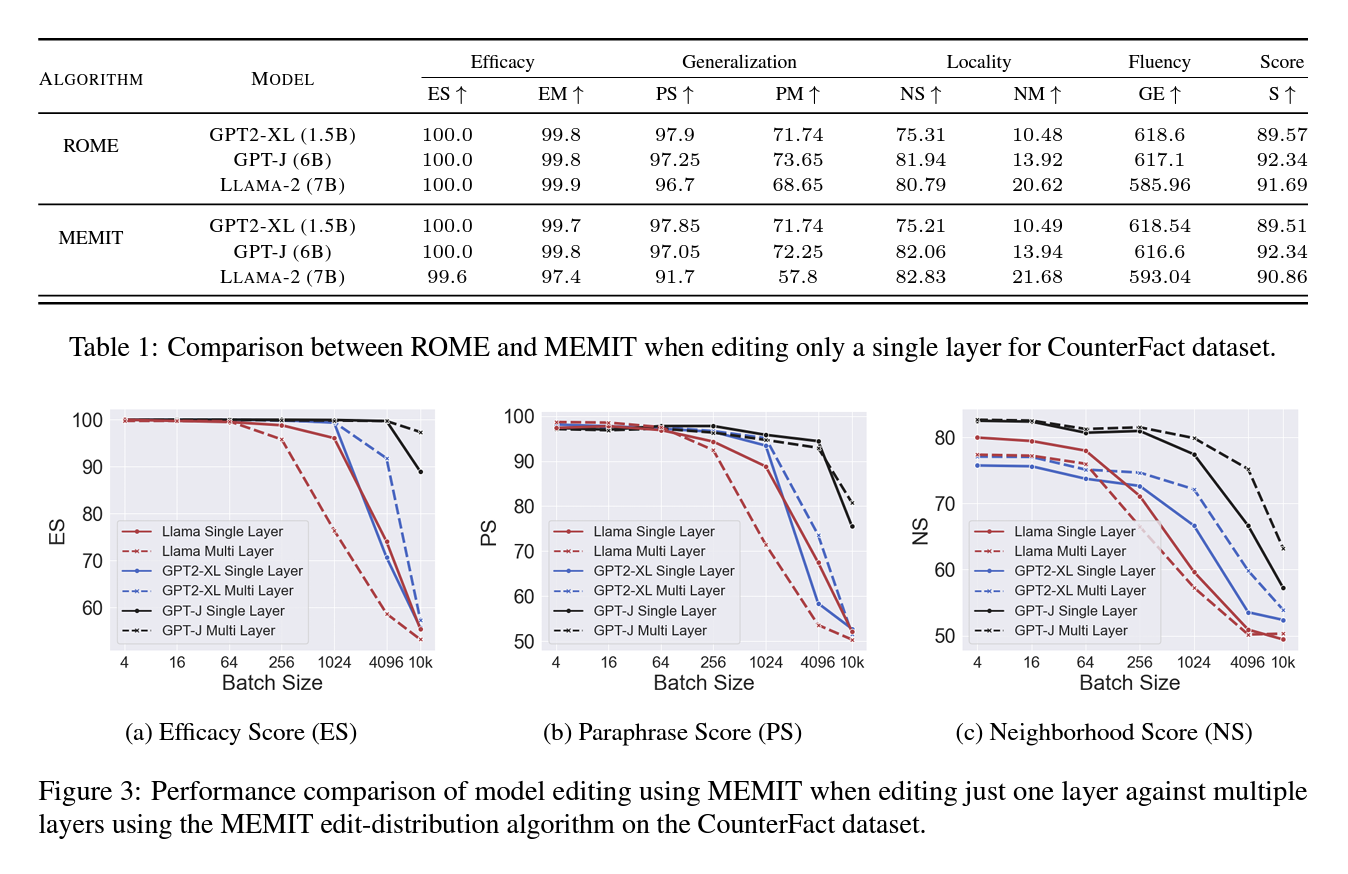
Introducing EMMET

EMMET provides a closed-form solution for batched-editing under equality constraints, creating a batched version of ROME.

According to the preservation-memorization objective, we want to find new weights \( \hat{W} \) for a weight matrix \( W_0 \) such that:

This equation is solved using Lagrange multipliers. The Lagrangian for multiple equality constraints is:

To solve this system of equations, we set \( \frac{\delta L}{\delta \hat{W}} = 0 \):

where \( \Lambda = [\lambda_1 \mid \lambda_2 \mid ... \mid \lambda_E] \) and \( K_E = [k_e^1 \mid k_e^2 \mid ... \mid k_e^E] \). Setting \( K_0 K_0^T = C_0 \) (assuming \( C_0 \) is invertible), the update equation for EMMET is:

The unknown matrix of Lagrange multipliers (\(\Lambda\)) is found using the constraint \( \hat{W} K_E = V_E \):

Replacing the above equation in the update equation gives us:

When \( E = 1 \), the \( K_E \) matrix reduces to a single vector \( k_e \), and the equation reduces to the ROME update equation (Equation 5). EMMET unifies ROME and MEMIT under the preservation-memorization objective, allowing for both batched and singular edits using equality constraints for memorization, similar to MEMIT's least-square based memorization.

Stabilizing EMMET

EMMET and MEMIT invert two critical matrices: \( C_0 = K_0 K_0^T \) and \( D = K_E^T C_0^{-1} K_E \). While invertibility is assumed, it's not always guaranteed. \( C_0 \) is a sum of outer products of key-vectors. For an LLM of dimension \( d \), key-vector dimensionality is usually \( 4d \). Thus, \( C_0 \) is invertible if it includes at least \( 4d \) independent vectors.

Example: For Llama-2-7b with a hidden dimension of 4096, key vectors have a dimensionality of 16384. Therefore, preserving at least 16384 independent key-vectors ensures \( C_0 \) is invertible. In practice, preserving a larger number of vectors almost always satisfies this condition.

\( D \) is a square matrix of dimensionality equal to the number of edits. If \( C_0 \) is invertible, \( D \) is invertible if \( K_E \) is full-rank, meaning all key-vectors for memorized facts are independent. Non-independent keys can be removed from batches to ensure invertibility. Although \( D \) is not usually non-invertible in practice, it often becomes ill-conditioned, leading to instability in numerical computations.

To counteract instability, \( D \) is modified to \( D + \alpha I \), with \( \alpha \) set to 0.1 based on ablation studies over various batch sizes. This adjustment ensures stable batched edits using EMMET.

Batch Editing with EMMET

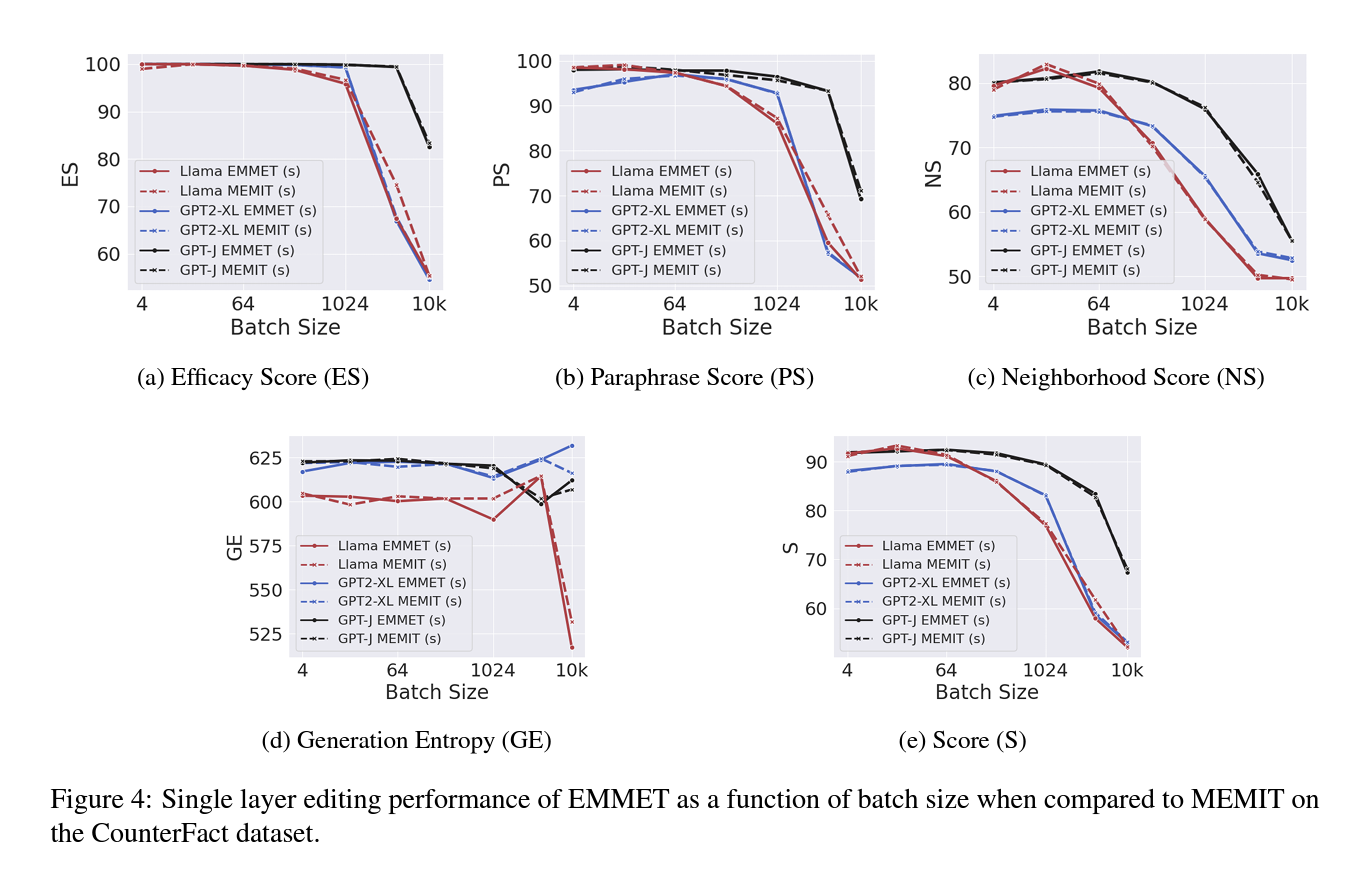
Experiments with EMMET on models like GPT2-XL, GPT-J, and Llama-2-7b show its performance across various batch sizes on datasets like CounterFact and zsRE. EMMET and MEMIT perform similarly on single-layer edits, with MEMIT slightly outperforming for Llama-2-7b.

Applying MEMIT's edit-distribution to EMMET shows slight performance improvements for EMMET on Llama-2-7b. Both algorithms successfully handle batched edits up to 10,000, leading to similar model degradation.

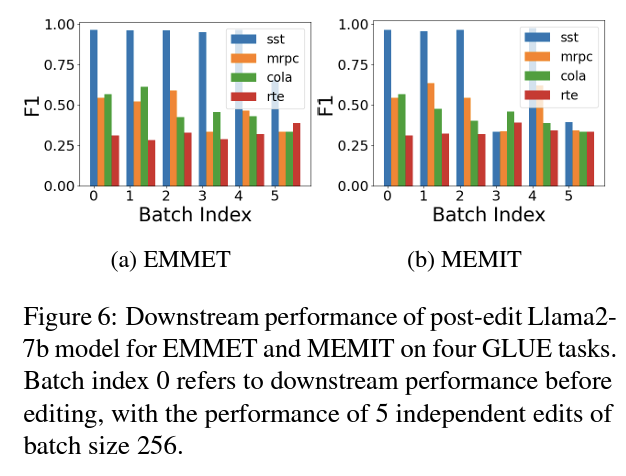
Downstream task evaluations using the GLUE benchmark and linguistic acceptability classification reveal similar degradation for both EMMET and MEMIT.

EMMET's theoretically stronger memorization constraint does not significantly improve editing efficacy over MEMIT, indicating potential limits of model editing under the preservation-memorization objective. EMMET remains a significant step in unifying model editing techniques, despite not outperforming MEMIT. Both methods exhibit robust performance and similar model degradation across large batch sizes.

Conclusion

This paper unites two popular model editing techniques, ROME and MEMIT, under the preservation-memorization objective. ROME performs equality-constrained edits, while MEMIT operates under a least-square constraint. The paper disentangles the edit-distribution algorithm in MEMIT from its optimization objective, emphasizing that future comparisons with MEMIT should focus on the objective rather than the algorithm. Additionally, the paper introduces EMMET (Equality-constrained Mass Model Editing in a Transformer), a new batched-editing algorithm based on the preservation-memorization objective with equality constraints for batched-memorization. Experiments show that EMMET performs similarly to MEMIT across various metrics, unifying model editing under the preservation-memorization framework. This unifying framework aims to improve the understanding of these algorithms and encourage future research based on both intuition and mathematics.

Limitation & Ethical Consideration

This paper unites two popular model editing techniques, ROME and MEMIT, under the preservation-memorization objective. ROME performs equality-constrained edits, while MEMIT operates under a least-square constraint. The paper disentangles the edit-distribution algorithm in MEMIT from its optimization objective, emphasizing that future comparisons with MEMIT should focus on the objective rather than the algorithm. Additionally, the paper introduces EMMET (Equality-constrained Mass Model Editing in a Transformer), a new batched-editing algorithm based on the preservation-memorization objective with equality constraints for batched-memorization. Experiments show that EMMET performs similarly to MEMIT across various metrics, unifying model editing under the preservation-memorization framework. This unifying framework aims to improve the understanding of these algorithms and encourage future research based on both intuition and mathematics.

While our technique streamlines error correction processes, it does not address deeper structural limitations within models, such as amplifying existing errors or introducing new inaccuracies. The effectiveness of our method varies with the model architecture and the nature of the edited knowledge. Despite a theoretically stronger memorization objective, EMMET does not outperform MEMIT, indicating a potential saturation point for model editing with current approaches. This underscores the need for further research into edit distribution and its implications. Our work enhances understanding of model behavior but must be interpreted with awareness of these limitations.

While our model editing method effectively corrects errors or updates facts in models, it raises concerns about potential misuse, such as inserting harmful or false knowledge. Therefore, LLMs should not be considered reliable knowledge bases, and caution is warranted in their use.